Viro Patchworking
Viro.sage is a Python class for using Viro Patchworking from within the computer algebra system Sage, written by Timo de Wolff, Emma Owusu Kwaakwah and Christopher O'Neill.
  • The code is used via two classes: ViroComplex (for Viro's original construction) and CIViroComplex (for Sturmfel's generalization to complete intersections). See the sample code below.
  • Autocomplete is supported in the Sage web interface, i.e. typing 
    viro.<TAB>
    will give a list of available functions. Again, see the sample code below.
  • The handy triangulation picker provides a graphical interface for building triangulations and sign labelings.
  • Comments and feature requests are encouraged, just send the authors an email!
Please note that this is a beta version and subject to change without notice.
Download
Given below is a current version of Viro.sage. Changes from the previous version can be found here.
  • Viro.sage (version 0.5b), posted Sep 7, 2021
Viro.sage is released under the terms of the MIT license. The MIT License is simple and easy to understand and it places almost no restrictions on what you can do with this software.
Action shots
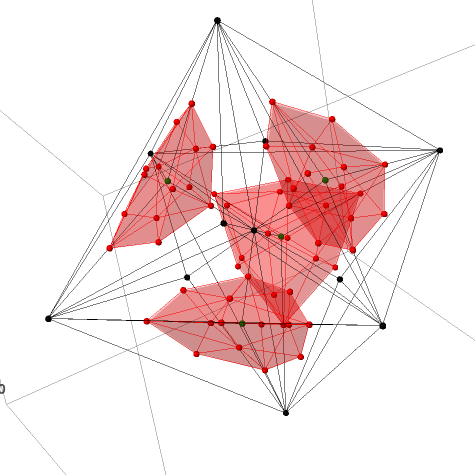
The figure below depicts several plots produced by Viro.sage.
  • Upper left: a hypersurface example in 2 variables.
  • Upper right: a counterexample to the Ragsdale conjecture due to Viro and Itenberg.
  • Lower left: a complete intersection example in 2 variables due to Sturmfels.
  • Lower right: a hypersurface example in 3 variables.
Usage
To set up your machine to use Viro.sage, do the following.
  • First, install Sage on your machine. Instructions for doing so can be found here.
  • Next, download Viro.sage at the link above, and place it in your favorite folder.
The following code fragment gives an overview of how to use the ViroComplex and CIViroComplex classes from within Sage. More complete documentation is now available in the Viro.sage source file. 
sage: load('/PATH_TO_FILE/Viro.sage')

sage: ragsviro = ViroComplex.RagsdaleCounterexample()
sage: print ragsviro.ViroComplex()
Simplicial complex with 610 vertices and 600 facets
sage: ragsviro.Homology()
{0: Z^43, 1: Z^34}
sage: ragsviro.Plot()

sage: curvelist=[[[(0,3),0,1], [(1,2),1,-1], [(2,1),5,-1], [(3,0),12,1], 
                  [(0,2),1,-1], [(1,1),4,1], [(2,0),9,-1], [(0,1),5,-1], 
                  [(1,0),9,-1], [(0,0),12,1]], 
                 [[(0,2),8,1], [(1,1),6,-1], [(2,0),6,1], [(0,1),3,-1], 
                  [(1,0),2,-1], [(0,0),0,1]]]
sage: civiro = CIViroComplex.FromBigLists(curvelist)
sage: print civiro.ViroComplex()
Simplicial complex with 6 vertices and 6 facets
sage: print civiro.Homology()
{0: Z^5}
sage: civiro.Plot()

viro3d = ViroComplex.FromLists([(4,0,0),(0,4,0),(0,0,4),(1,1,1),(0,0,0),(1,2,2)],[1,1,1,1,1,-1], [2,2,2,1,2,1])
print viro3d.ViroComplex()
viro3d.Plot()